算法

二叉排序树

1、二叉排序树的介绍

二叉排序树：BST: (Binary Sort(Search) Tree), 对于二叉排序树的任何一个非叶子节点，要求左子节点的值比当前节点的值小，右子节点的值比当前节点的值大
特别说明：如果有相同的值，可以将该节点放在左子节点或右子节点

2、二叉排序树添加节点

思路：
根据插入节点的值来寻找其应该插入的位置
新插入的节点都是叶子节点

3、添加节点代码实现

  public void add(Node node){
        //节点为空时，结束递归
        if (node == null){
            return;
        }
        //比当前的值大，挂到右节点
        if (node.value > this.value){
            if (this.right == null){
                this.right = node;
            }else {
                this.right.add(node);
            }
        //小于或等于当前值，挂到左边的节点
        }else {
            if (this.left == null){
                this.left = node;
            }else {
                this.left.add(node);
            }
        }
    }

4、二叉排序树的遍历

思路：
二叉排序树的特性是，左子节点比当前节点的值小，右子节点比当前节点的值大，所以遍历采用中序遍历，这样就能从小到大进行排序

5、二叉排序树的遍历代码实现

//中序遍历树
    public void infixOrder(){
        if (this.left != null){
            this.left.infixOrder();
        }
        System.out.println(this);
        if (this.right != null){
            this.right.infixOrder();
        }
    }

6、二叉排序树节点的删除

思路：
删除叶子节点（没有子节点）
找到待删除的节点
找到待删除节点的父节点
判断待删除节点是其父节点的左孩子还是右孩子，然后把值置为空
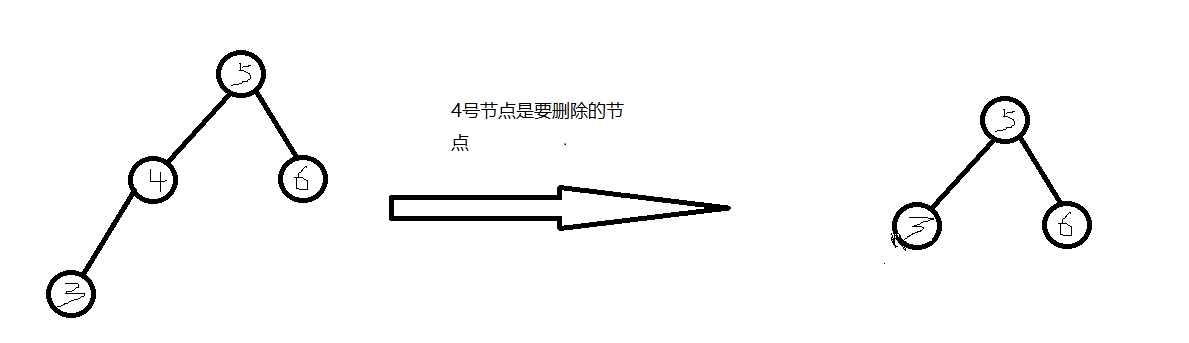
删除只有一颗子树的节点（如删除值为1的节点）
找到待删除的节点，记为delNode
找到待删除的节点的父节点parentNode
判断delNode是parentNode的左孩子还是右孩子
判断delNode中有个左孩子还是右孩子节点
让原本parentNode下的delNode节点指向delNode的孩子节点
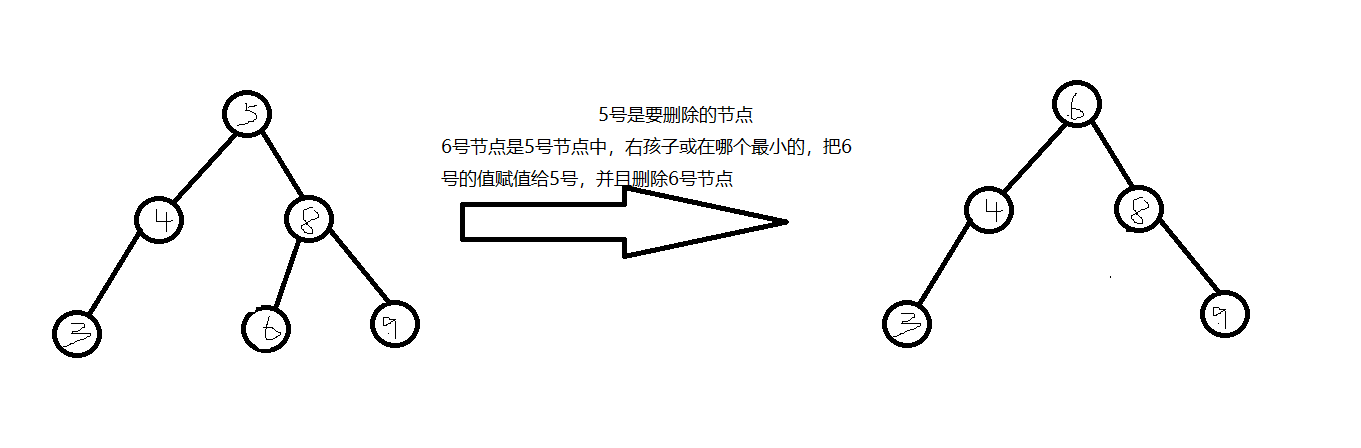
删除有两颗子树的节点（如删除值为3的节点）
找到待删除的节点delNode
找到待删除的节点的父节点parentNode
判断delNode节点是parentNode的左孩子还是右孩子
顺着delNode节点的右子树(从右孩子所有的节点中，包括右孩子的所有子节点)，找到一个值最小的节点（该值的大小最接近待删除节点的值）
把刚刚找到的那个值，替换掉delNode节点的值，并删除那个值所在的节点

7、删除节点代码实现

没按照尚硅谷的写，用自己的思路写出来的，按照注释去看，应该是能看懂的

package com.yishuai.BinarySortTree;

/**
 * @author yishuai
 * @description 二叉排序树
 * @date 2021/3/30 15:53
 */
public class BinaryTreeDemo {
    public static void main(String[] args) {
        int[] arr ={5,3,1,7,4,9,2,8,6};
        BinaryTree binaryTree = new BinaryTree();
        for (int i = 0; i < arr.length; i++) {
            //将数组所有的数，都新建一个节点，挂到树上
            binaryTree.add(new Node(arr[i]));
        }
        System.out.println("中序遍历后的结果是：");
        binaryTree.infixOrder();
        //删除叶子节点
        binaryTree.delNode(3);
        System.out.println("删除后中序遍历结果是：");
        binaryTree.infixOrder();
    }
}

class BinaryTree{
    //root节点
    private Node root;

    public BinaryTree(Node root) {
        this.root = root;
    }
    public BinaryTree() {
    }
    //添加节点
    public void add(Node node){
        //如果root节点是空的，就把当前节点作为root节点
        if (root == null){
            root = node;
        }else {
            root.add(node);
        }
    }
    //中序遍历
    public void infixOrder(){
        root.infixOrder();
    }
    //查找要删除的节点
    public Node findNode(int value){
        if (root == null){
            return null;
        }
        return root.findNode(value);
    }
    //查找要删除节点的父节点
    public Node parentsNode(int value){
        if (root == null || (root.left == null && root.right == null)){
            return null;
        }
        return root.parentsNode(value);
    }
    //删除节点
    public void delNode(int value){
        if (root == null){
            return;
        }
        Node node = root.findNode(value);
        Node parentsNode = root.parentsNode(value);
        //没找到要删除的节点，直接返回
        if (node == null){
            System.out.println("没找到要删除的节点");
            return;
        }
        //左右节点都是空，代表是叶子节点，直接删除即可
        if (node.left == null && node.right == null){
            if (parentsNode.left !=null && parentsNode.left.value == value){
                parentsNode.left = null;
            }else if(parentsNode.right != null && parentsNode.right.value == value){
                parentsNode.right = null;
            }
            //父节点的左边节点，且被删除节点只有一个左孩子的节点
        }else if((node.left != null && node.right == null) && parentsNode.left.value == node.value){
            parentsNode.left.value = node.left.value;
            node.left = null;
            //父节点的左边节点，且被删除节点只有一个右孩子的节点
        }else if ((node.right != null && node.left == null) && parentsNode.left.value == node.value){
            parentsNode.left.value = node.right.value;
            node.right = null;
            //父节点的右边节点，且被删除节点只有一个左孩子的节点
        }else if((node.left != null && node.right == null) && parentsNode.right.value == node.value){
            parentsNode.right.value = node.left.value;
            node.left = null;
            //父节点的右边节点，且被删除节点只有一个右孩子的节点
        }else if((node.right != null && node.left == null) && parentsNode.right.value == node.value){
            parentsNode.right.value = node.right.value;
            node.right = null;
            //左右节点都不为空，则取右边最小的数
        }else if(node.right !=null && node.left != null){
            //找到右孩子中最小的节点
            Node rightSmallNode = node.getRightSmallNode(node.right);
            //找到这个最小值节点的父节点
            Node smallParentsNode = node.parentsNode(rightSmallNode.value);
            //取到最小的节点，覆盖到当前节点
            node.value = rightSmallNode.value;
            //删除最小的节点
            if (smallParentsNode.left.value == smallParentsNode.value){
                smallParentsNode.left = null;
            }else {
                smallParentsNode.right =null;
            }

        }

    }

}


class Node{
    //用来标记节点的值，也是标记几号节点
    int value;
    Node left;
    Node right;
    public Node(int value) {
        this.value = value;
    }

    public Node() {
    }

    @Override
    public String toString() {
        return "Node{" +
                "value=" + value +
                '}';
    }

    //添加节点
    public void add(Node node){
        //节点为空时，结束递归
        if (node == null){
            return;
        }
        //比当前的值大，挂到右节点
        if (node.value > this.value){
            if (this.right == null){
                this.right = node;
            }else {
                this.right.add(node);
            }
            //小于或等于当前值，挂到左边的节点
        }else {
            if (this.left == null){
                this.left = node;
            }else {
                this.left.add(node);
            }
        }
    }

    //中序遍历树
    public void infixOrder(){
        if (this.left != null){
            this.left.infixOrder();
        }
        System.out.println(this);
        if (this.right != null){
            this.right.infixOrder();
        }
    }

    //查找要删除的节点
    public Node findNode(int value){
        if (this.value == value){
            return this;
        }else if(this.value > value){
            if (this.left == null){
                return null;
            }
            //比当前的值小，向左查找
            return this.left.findNode(value);
        }else {
            if (this.right == null){
                return null;
            }
            //小于或等于当前值
            return this.right.findNode(value);
        }
    }

    /**
     * 查找要删除节点的父节点
     * @param value 要删除的节点
     * @return 找到了则返回这个父节点，没找到返回null
     */
    public Node parentsNode(int value){
        //左节点或右节点的值为要查找的值
        if (this.left != null && this.left.value == value || this.right != null && this.right.value == value){
            return this;
        }else {
            //遍历左子节点
            if(this.left != null && this.value > value){
                return this.left.parentsNode(value);
            //遍历右子节点
            }else if(this.right != null && this.value < value){
                return this.right.parentsNode(value);
            }else {
                return null;
            }
        }
    }

    //取右子树中最小的节点
    public Node getRightSmallNode(Node node){
        if (node.left != null){
            return node.getRightSmallNode(node.left);
        }else{
            return node;
        }
    }
}

如果觉得文章对你有用，请随意赞赏

算法

二叉排序树

http://192.168.0.251:2081/archives/er-cha-pai-xu-shu

作者

Administrator

发布于

2023-11-13

更新于

2024-10-13

许可协议

CC BY 4.0